In mathematics, the factorial of a non-negative integer n, denoted by n!, is the product of all positive integers less than or equal to n. For example,
5! = 5 * 4 * 3 * 2 * 1 = 120.
The value of 0! is 1, according to the convention for an empty product.
The factorial operation is encountered in many areas of mathematics, notably in combinatorics, algebra, and mathematical analysis. Its most basic occurrence is the fact that there are n! ways to arrange n distinct objects into a sequence (i.e., permutations of the set of objects). This fact was known at least as early as the 12th century, to Indian scholars. Fabian Stedman in 1677 described factorials as applied to change ringing.
5! = 5 * 4 * 3 * 2 * 1 = 120.
The value of 0! is 1, according to the convention for an empty product.
The factorial operation is encountered in many areas of mathematics, notably in combinatorics, algebra, and mathematical analysis. Its most basic occurrence is the fact that there are n! ways to arrange n distinct objects into a sequence (i.e., permutations of the set of objects). This fact was known at least as early as the 12th century, to Indian scholars. Fabian Stedman in 1677 described factorials as applied to change ringing.
Information source: wikipedia.org
Program:->
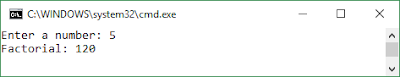 |
| Output |
#include <stdio.h>
#include <conio.h>
int main() {
int x,f=1,i;
printf("Enter a number: ");
scanf("%d", &x);
for (i = 1; i <= x; ++i)
{
f=f*i;
}
printf("Factorial: %d\n",f);
return(0);
}













0 comments :
Post a Comment